Zippers 2: Building a Rose Tree Zipper

As a follow up to my post about Zippers for lists and binary trees, I wanted to create a zipper for a slightly more complex data structure. The Rose Tree is a tree structure where the number of branches a node may have is variable. An example of a rose tree would be the directory structure on your computer: each directory may contain 0 or more sub directories which, in turn, may contain addition subdirectories. With this example in mind, the zipper is analagous to you moving through your computers file system: starting at the root directory and using cd to move down a branch and cd .. to move back.

Rose Tree Implementation

The implementation of a rose tree is pretty simple. It’s just like a binary tree but, instead of each node having two branches, each node has a list of branches:

type RoseTree<'a> =
  | Empty
  | RoseTree of 'a * (RoseTree<'a> list)

The zipper of the rose tree, however, is a lot more interesting and fun. It’s basically a combination of the binary tree zipper and the list zipper: you need a tree zipper to keep track of where in the tree you are by level and a list zipper to keep track of where in the each node’s list of branches you are.

Algebraicly, the rose tree is: $$R = 1 + a\cdot L(R)$$

Where $$L(R)$$ is a list of rose trees.

The derivative is:

\[ \begin{eqnarray} \partial_aR &=& L(R) + a\partial_aL(R)\partial_aR \\
\partial_aR - a\partial_aL(R)\partial_aR &=& L(R) \\
(1 - a\partial_aL(R))\partial_aR &=& L(R) \\
\partial_aR &=& \frac{L(R)}{1-a\partial_aL(R)} \\
&=& L(R)\frac{1}{1 - a\partial_aL(R)} \\
&=& L(R)L(a\partial_aL(R)) \\
&=& L(R)L(aL^2(R)) \\
\end{eqnarray} \]

The next to last step uses the identity $$L(a) = \frac{1}{1 - a}$$ to arrive at $$L(R)L(aL^2(R))$$.

This translates to the type:

type RoseTreeZipper<'a> = 'a * RoseTree<'a> list * (('a * RoseTree<'a> list * RoseTree<'a> list) list)

and that looks pretty insane.

However, it does make sense. Here’s the break down. The first part 'a is the value of the current node and the RoseTree<'a> list is the list of branches at this node. So, together 'a * RoseTree<'a> list is the cursors current position in the rose tree.

Now here’s the break down for ('a * RoseTree<'a> list * RoseTree<'a> list) list. This is a list of the previous positions the cursor had in the rose tree, just like we saw with the binary tree zipper. The 'a is the value of the node the cursor used to point at. The tuple RoseTree<'a> list * RoseTree<'a> list is all the branches of the node except where the cursor is currently at! The first RoseTree<'a> list is the branches to the left of the branch down which the cursor went and the second RoseTree<'a> list is all the branches to the right!

To help clarify how the rose tree zipper works, here’s a visual explanation.

The color green indicates the position of the cursor.

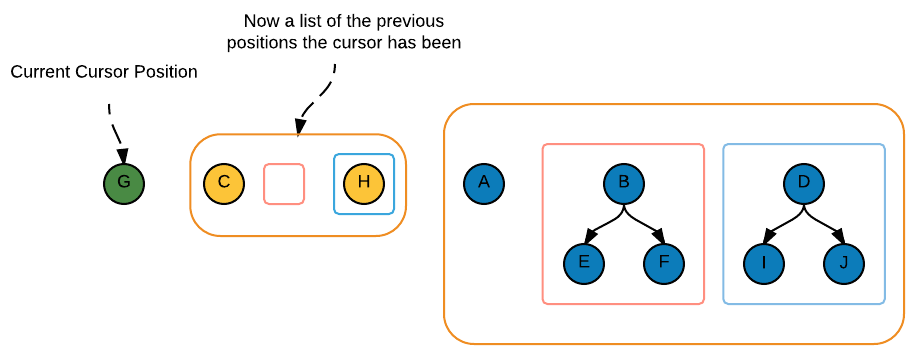
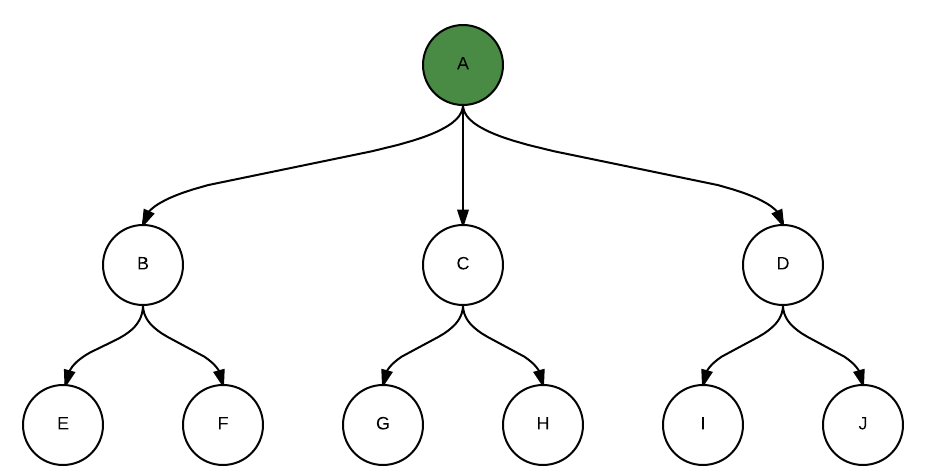
Here we are with a newly created zipper on a rose tree. The cursor is pointing to the root of the tree

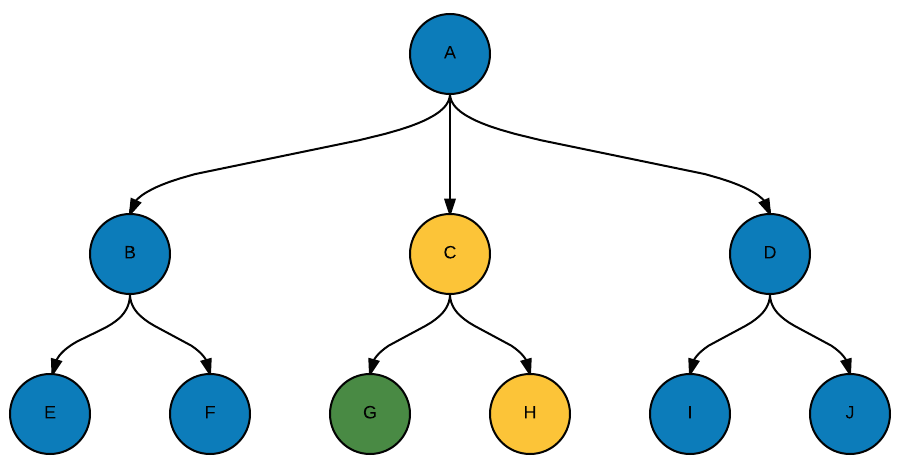
We’ll move the cursor down to the middle branch. The root of the tree and the left and right branches are then moved into the history list for the cursor. The color blue is used to show that all those nodes are grouped together as one entry in the history list. 

Here’s a visual of the rose tree zipper value after the cursor is moved to the middle node. The cursor points to (C, [G; H]), corresponding to the 'a * RoseTree<'a> list in the zipper type. The previous cursor position corresponds to the list of 'a * RoseTree<'a> list * RoseTree<'a> list.

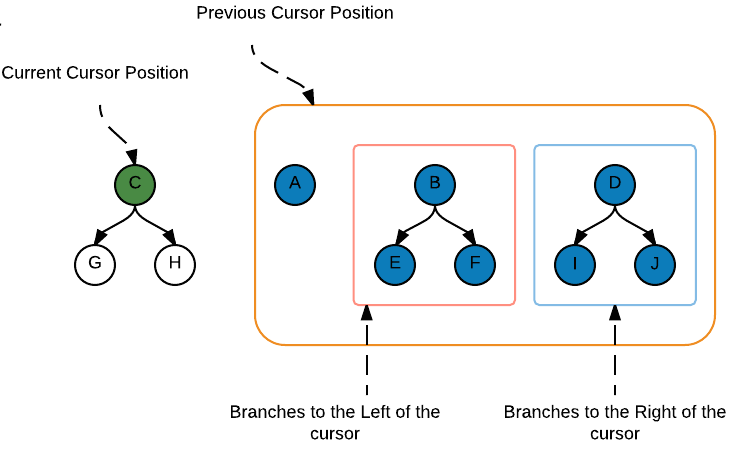
Moving the cursor down the left branch, the previous node and the right branch are colored to indicate that they are grouped together and prepended to the history list.

Visualizing the new rose tree zipper value. C, H have been moved to the head of the history list. H is moved into the list of branches to the right of where the cursor is. The list of branches to the left is empty, since this subtree only had two branches. C is moved into the node value of the entry.